Byzantine agreement algorithms and Dolev Strong

Why do we need consensus?

Spacemesh is a new blockmesh infrastructure based on a directed acyclic graph (DAG). Using this kind of block structure allows Spacemesh many great things in terms of our mining fairness and the delivery of our promise to ensure actual decentralization. There are really a lot of good things that this structure allows - topics we shall open in a future post.

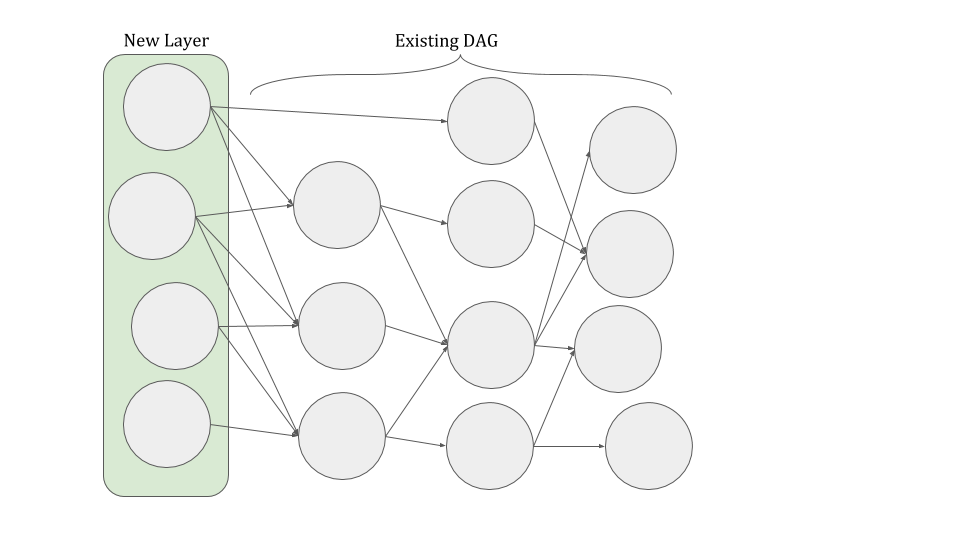
Alongside the many advantages of DAG, there is one main challenge it poses to decentralized systems: how do we keep the same image of the mesh graph on all nodes? Network issues, attackers or misconfigured nodes can disrupt the network and create inconsistencies in the graph between nodes.

For example, let’s assume that Alice and Bob are honest nodes in the network and that Eve is an adversary node that wishes to force a fork upon the graph. To do so, she sends the values {a,b,c} as the next extension of the graph to Alice, and values {x,y,z} to Bob. Now Bob and Alice have different images of the mesh graph. To prevent this, nodes extending the network must reach consensus on what the correct blocks are to insert into the DAG at a time. Each node must have the same list of new blocks to be inserted into the layer, and only after reaching consensus upon this list can the graph be further extended.

A good consensus algorithm must prevent a malicious sender from introducing a new message into the exchange, claiming to have received it from another. It must also allow senders to sign a message in a way that the receivers can verify that the message is authentic and originated from the sender. Senders should not be able to forge the signature of other senders; thus no one can change the contents of a message other than its original author.

The Bitcoin consensus algorithm is pretty straightforward: not all blocks produced go into the blockchain, and basically the longest chain wins, whoever succeeds in creating the next proof of work first can extend the chain with its block, and all other produced blocks at the same height are discarded. All that mining and energy spent for nothing.

Our consensus protocols should keep all nodes synchronized and withstand attacks designed to fork the graph. To do so, we have two algorithms. The first is a faster consensus algorithm that achieves agreement upon the layer that is now being created, and is fondly named the “hare” protocol; the other, slower algorithm is for validating the entire graph and “mending” attack attempts and graph inconsistencies, and fondly named the Tortoise. It also enforces the graphs irreversibility, on which I’ll elaborate in a different post. The hare protocol’s purpose is to reach consensus regarding the layer that is now being built, meaning which blocks should go into the layer. Each eligible node publishes a block to other eligible nodes in a certain time frame; after this time frame has elapsed, all nodes must reach consensus about the blocks they’ve received from other nodes, and these are the blocks that will form the next “layer.”

So how do we decide which block goes into the graph when we don’t have a simple decision-making criteria, such as chain length and PoW validity? For these we use Byzantine fault tolerance (BFT) protocols, which will be explained below…

Byzantine fault tolerance protocols are algorithms that allow all actors to reach an agreement on a message or a state within a network of actors, which can contain faulty or even malicious actors. The name of these algorithms originates from the Byzantine Generals problem:

This problem describes a scenario in which several generals in command of their legions place a city under siege and need to decide whether they should attack it or retreat. Since the siege entails the generals to plant their legions in different locations around the outskirts of the city, the only way for the generals to communicate between themselves is by using couriers. The generals must reach a unanimous decision on whether to attack or not, since a partial attack of the city will result in the troops being outnumbered by the city guards and the entire army falling apart. To make things more complicated, some of the generals are traitors and wish for the defeat of the entire army. The traitors may send malicious messages to different generals and disrupt the correlated attack. To complicate even more, some couriers may lose their way on the badly marked network of roads, so some of the messages may not reach their intended targets. Reaching agreement, as it seems, on whether to attack or not, seems rather more complicated than what one may have initially thought.

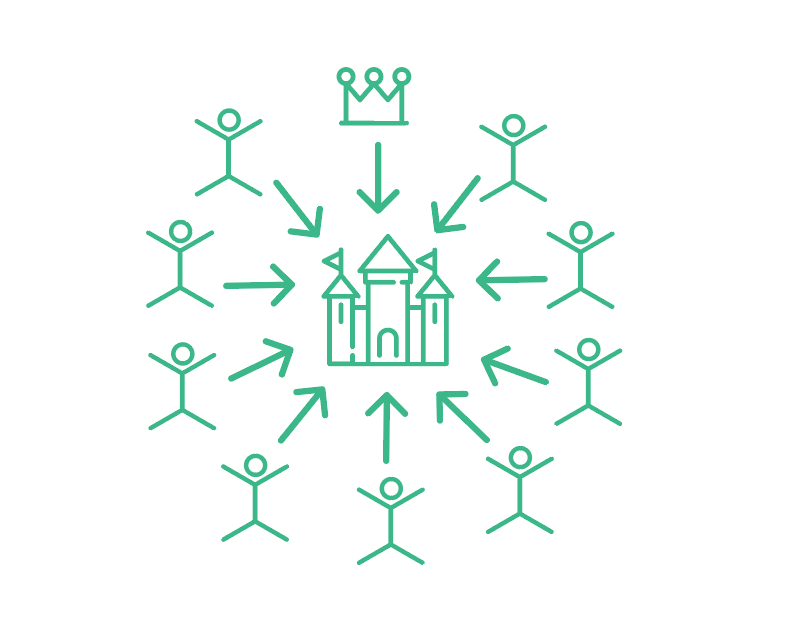
Coordinated attack leading to victory

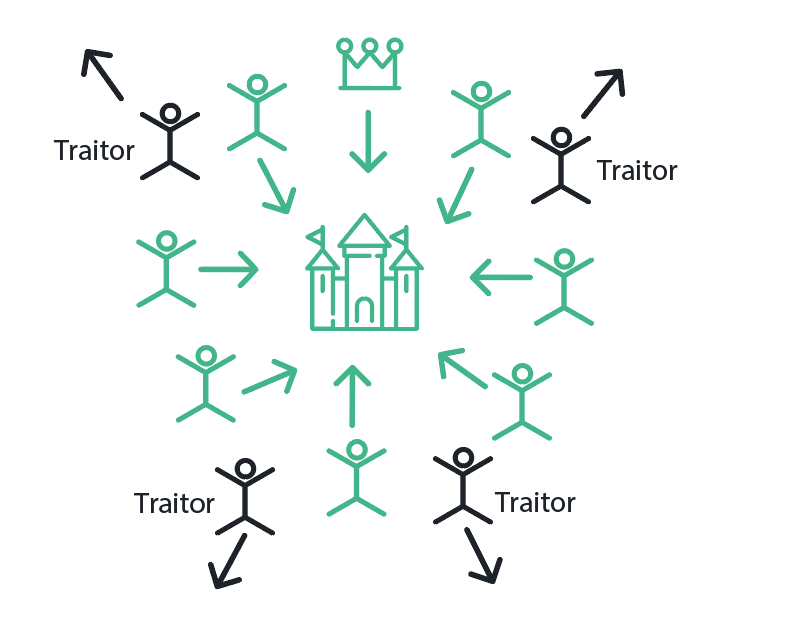
Uncoordinated attack leading to defeat

To overcome these kinds of attacks (or network faults) and to make sure adversaries can’t compromise the correctness of our DAG, we use a Byzantine agreement algorithm called Dolev Strong.

Dolev Strong was first designed by Danny Dolev and H.Raymond Strong. It was our first attempt to implement this algorithm to reach consensus between our nodes. The algorithm’s objective is to allow honest parties to reach a consensus upon a certain message, while coping with malicious nodes in the network. Dolev Strong is a time-based consensus protocol. It requires all nodes to start transmitting and receiving messages at the same time. It is described as a network of one sender and multiple receivers.

The algorithm runs in rounds, and requires clocks to be synchronized between all participating nodes. Each round begins at a constant time-frame in which receivers can pass along a message. The algorithm must run for t +1 number of rounds - where t is the number of adversary or faulty nodes we can have in our network without failing to reach consensus upon a message (t is the constant that describes the basic network security assumption).

A simple pseudocode of the algorithm:

bool isValid(message, i) {
	set signatures
	if (message.signatures.count != i) {
		return false
	}
	If (message.signatures.contains(origin_sig) != true){
		Return false
	}
	for (sign in message.signatures) {
		if (signatures.contains(sign)) {
			return false
		}
		signatures.add(sign)
	}
	return true
}

void phase(i) {
	for (msg in INCOMING_MESSAGES) {
		if (VALUES.count == 2) {
			return
		}
		if (isValid(msg)) {
			if (message.sender == SENDER) {
				VALUES.add(msg.value)		
			}
			sign_and_send_all_but_signed_processors(msg)
		}
	}
	if (i == t+1) {
		if (VALUES.count == 1) {
			return VALUES[0]
		}
		return 0
	}
}

In our implementation, each node is a sender and also a receiver for other agreement attempts upon messages from other eligible nodes. We employ a standard modern cryptographic signature scheme to authenticate message sender and to prevent message content modifications by man-in-the-middle kinds of attacks.Whenever a sender wishes to reach consensus on a certain payload within a network of other receiving nodes, the payload and the sender’s public key are signed using the sender node’s private cryptography key and the signature is added alongside the payload. This enables receiving nodes to validate the content and origin of this message.

Each node that receives a message validates the content using the signatures found chained after the payload, and then signs the payload with its own private key.
After chaining the node’s signature to all other signatures, the node then sends the message to all nodes in the layer that have not yet signed it yet.
If a receiver receives two contradicting messages from the same sender, this sender is considered malicious, in which case the receiver will forward the message to all other nodes to notify them of the malicious sender so they can stop processing messages from it.
A message is also considered invalid if the number of signatures is less than the current round number.
At the end of a t +1 round iteration, all nodes should reach consensus on a message, unless the sender was faulty, in which case the consensus is that its messages are invalid.

This is the outline of first algorithm we’ve implemented. In my next blog post I’ll dive into the implementation details, the problems we’ve encountered during this implementation and the lessons learned.